The argument of a complex number is the angle the number makes with the real axis when it is plotted on an argand diagram:
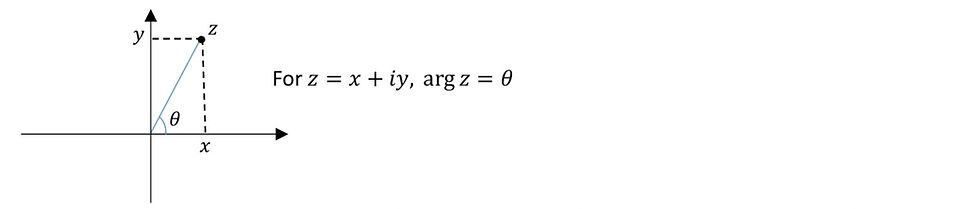
In many places, you will find a formula for the argument of a complex number. Often this formula is given as:
In order to construct a correct general formula, we need to consider negative values too.
Can we somehow amalgamate these three separate formulae into one? To do that we would have to try to come up with a way of generating the following rules:
Notice that this formula won’t work for the negative real axis (z=-k) as then the first term becomes 0/0 which is undefined. But other than that, it works very nicely.
So as you can see, the formula that you see on websites and in books just requires an extra term and some different boundary conditions. The extra term is an interesting object as it is always just pi, minus pi or zero depending on which quadrant the number is in. This is not a particularly pleasant looking formula, and it is probably easier to work out the argument using the ‘common sense’ approach, but at least it works!
I'll write another article on finding a formula for the argument of a complex number another time, but next time I'll take a rather different, altogether more cunning approach!
ความคิดเห็น